Flat Earth? Doing the Math

Throughout the day, rapper B.o.B. has been tweeting "evidence" that the earth is flat, making him the most recent face of a growing flat earth movement. The ancient Greeks deduced that the earth is round by recognizing that the earth always casts a circular shadow on the moon and were even able to make a reasonably good approximation of the radius of the earth. Nearly 2,400 years later, it seems we should have universal consensus on the shape of the earth, especially since a live stream of the earth from space is just a click away.

What can account for the resurgence of flat earth truthers? B.o.B.'s question to Neil deGrasse Tyson, who had responded to some of the flat earth "evidence", is telling: "r u a mason?". Those who advocate for a flat earth are not just making a scientific claim, they're making the claim that the government, NASA, and the scientific community are controlled by an elite group attempting to systematically deceive the public on the nature of the cosmos. Moon landing: faked. Scientific authorities: compromised. Everybody else: sheep. Except, of course, that guy on YouTube who posted a video that exposes the whole thing. Pay some money and you can get his book on it, too.

This suspicion of scientific findings makes it very difficult to falsify the belief. Every piece of evidence one presents can simply be dismissed as part of the conspiracy. It makes for an interesting challenge: can one demonstrate that the earth is round without appealing to any modern authorities. (The ancient argument of the Earth's shadow on the moon is countered by a belief in an "anti-moon" that instead casts the shadow. It seems the ultimate conspiracy would be if a group of flat earthers faked a landing on this supposed anti-moon to prove its existence.)

Having posted a number of pictures that B.o.B. claimed demonstrated the non-curvature of the earth, a few hours ago he posted the challenge:

As a math guy, this caught my eye. It turns out the math required is just some basic high school geometry, making the flat earth movement the latest indicator that we need to do a much better job at improving our nation's math literacy. Here's one step in that direction.

New York Skyline

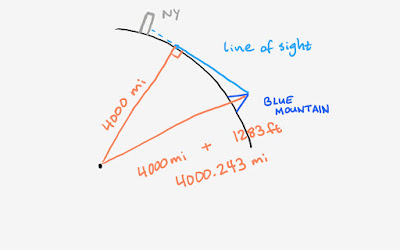
First of all, although the driving distance from Bear Mountain to Manhatten is 50 or 55 miles, it's only 40 miles away (map). Also, we'll be generous and approximate the earth to have radius 4000 miles (it is actually a bit less, but this will only bias the numbers in the flat earther's favor). So, how does the curvature of the earth affect one's view of the skyline? This diagram may help:

Notice when standing on top of blue mountain your line of sight only runs for so far until the curvature of the earth begins to obstruct your view. Using the Pythagorean Theorem we can calculate that distance to be 44.091 miles. Since New York is within 44 miles of Blue Mountain, on a clear day we can expect to see the entire skyline, just as the photo demonstrates.

But what if New York was 60 miles away? (Again, it's not. We're just running a hypothetical now.) We'd still be able to see the buildings, but the bottom portion would be hidden by the curvature of the earth. We can go ahead and calculate just how much would be hidden:

Another application of the Pythagorean Theorem gives us that just shy of 150 ft of the buildings would be covered (not too far off from B.o.B.'s claim of 170 ft). Notice, since many of the buildings in New York are many times that height, we would still expect to see the skyline.

Philadelphia Skyline

We can test other skyline claims similarly:

If you use the numbers given, then indeed we find that the lower 335 feet of the buildings should be hidden; however, since many buildings in Philadelphia are far taller than this, we should still expect to see the skyline. However, again the distance to the city has been overstated. The driving distance is less than 35 miles and the actual distance is closer to 30 miles (map). Being generous and using 35 miles takes the amount blocked to 200 feet. Interestingly, there happens to be a 60 foot fire tower on top of the hill. Standing on top of it, and using the actual distance to the city, it turns out less than the bottom 100 ft of the skyline is blocked by the earth's curvature. I encourage the interested reader to run the numbers for herself on other skyline photos that claim to prove the earth isn't curved.

Where's the Curve?

This'll be the last claim I engage with, bringing us full circle (like... a trip around the earth). Another application of Pythagorean's theorem shows us over a distance of 16 miles, the earth curves just shy of 170 ft. For perspective, the skyscrapes in those cities that you can barely see are many times that height. To think about it another way, the difference between the direction the skyscrapers are pointing in one city with the direction they're pointing in the other is 0.21°--a fraction of a degree. You see, the earth is big: just shy of 25,000 miles in circumference. So while the earth is curved, indeed, it is tough to notice on the scales that we're used to, although it is easily noticeable on a high altitude flight such as a concorde.

Many of the other arguments that B.o.B. posted are explained on the basis of misinformation (you can't see Polaris as you move into the southern hemisphere) or are based on a misunderstanding of science (how gravity works, what we mean when we call the earth an oblate spheroid, and so on). A good place to learn up on some of the relevant science is here and here.

Scripture and Science

Recently, I've had a few conversations with some friends about the relationship between science and scripture. They left me disheartened. On the one extreme I found friends who, believing they were being faithful to scripture, systemically rejected nearly our entire body of well-established scientific discovery. On the other extreme, I found friends who thought that scripture has been proven outdated, unreliable, and little more than fairy tales in light of modern scientific findings. I'm not sure if it is balancing or disorientating to have friends with such diverse perspectives!

To be fair, most of my friends fall somewhere between these extrema: my Christian friends tend to hold a high regard for scientific discovery and a number of them are actively involved in it, and my non-Christian friends tend to at least recognize some value in the teachings of scripture.

Nevertheless, these conversations reminded me of a number of errors, both historically and presently, that have muddled peoples thinking on the relationship between scripture and science. Here I'd like to offer a brief sketch of what seem to be some of the most common ones.

Scripture, not Aristotle
Perhaps the most famous example cited to show that scripture is opposed to scientific discovery is the case of the Catholic Church's persecution of scientists such as Kepler and Galileo. After all, their arguments that the earth rotated the sun contradicted the Biblical account, right?

Not quite.

It turns out the history surrounding these men is rather more complex, and political, than a simple the-scientists-said-this-but-the-Bible-said-that. The politics of the matter aside, to understand some of the dynamics involved, one has to consider another actor on the stage of intellectual thought: Aristotle.

By the medieval ages, the Catholic Church had altogether embraced Aristotle and his works as authoritative. For instance, one can trace the enormous influence Aristotle's works had on theologians such as Thomas Aquinas. One place this came through was in the Church's understanding of Justification, that is, how one is made right with God. They had embraced Aristotle's view that "men become builders by building and lyreplayers by playing the lyre; so too we become just by doing just acts" (Nicomachean Ethics, II.1).

This became a central point of controversy in the Reformation when Luther and others argued that Scripture taught justification by faith in contrast to the position of the Church which they believed amounted to justification by works.

Aristotle didn't just write about ethics; he also offered a cosmology in which the earth was fixed and the sun rotated about it. True, the Church appealed to biblical accounts such as Joshua commanding the sun to stand still to argue against Kepler and Galileo's work, but they did this because they were reading Scripture with an Aristotelian lens. Significantly, Kepler and Galileo were both dedicated Christians and offered readings of Scripture entirely consistent with their discoveries, but these were rejected because they challenged the authority of Aristotle, and hence the Church. This also explains why Galileo's discoveries of spots on the sun or craters on the moon were so offensive. Nowhere did scripture claim that the moon or sun were without blemish, but Aristotle had.

In fact, at the time Kepler recognized this, even labeling himself "the Luther of astrology". The Protestant Reformation, replacing the authority of the Church and its reliance on the opinions of the Church Fathers with the study of the book of scripture itself, opened the way for the scientific revolution that replaced the authority of ancient figures such as Aristotle with the study of "the book of nature" itself. For more on this, check out The Bible, Protestantism, and Rise of the Natural Sciences.

I find in this history a warning to modern Christians: we need to be sure that the ideas that we're defending in the name of faithfulness to scripture are actually the most faithful reading of scripture and not just ideas that we've latched onto and glossed over with Biblical language from some other source.

Science, not Scientism
Just as some ideas are labeled as teachings of scripture that really shouldn't be, we can label some ideas as scientific that shouldn't be. My favorite example to highlight this is the statement by logician Bertrand Russell: "What science cannot tell us, mankind cannot know."

Now, Russell was a fine logician who really upset attempts to ground mathematics upon set theory in the early 20th century by considering a set with the paradoxical property that it contained as an element every set that was not a element of itself. That might sound odd and rather confusing, but Russell was demonstrating that the current rules of set theory could lead to contradictions (which we really seek to avoid in mathematics). In particular, one could ask if this set of his was an element of itself and reason that if it was, then it must not be, but if it wasn't, then it must be, either way giving a contradiction. The point being, this led to the need for mathematicians to be a bit more careful in how to think about and discuss sets to avoid this kind of contradiction.

Why is this relevant? Because analyzing Russell's statement--"What science cannot tell us, mankind cannot know."--leads to a very similar paradox of contradiction. All one needs to do is ask if we can know that Russell's statement is true. Suppose we can. Observe, Russell's statement is not a scientific one. It is outside the scope of what one will ever discover with the scientific method. Hence, by its own criteria we cannot know that it is true!

At best, this leaves the possibility that it is true, but that we can never know of its truth. It turns out to be a statement of faith--and a hopeless faith at that. There is not even the possibility that one day we could know if such a statement is true.

Russell's statement embodies what has been called scientism. We see it alive in the academy when disciplines such as the humanities are disregarded as unscientific and hence considered without value. Indeed, not every discipline conforms to the scientific method, but perhaps other fields of investigation--be it that of the historian, economist, or even a theologian--require different methodologies. In fact, even to consider such questions of truth and how we can know it moves us beyond the realm of physics into metaphysics. A scientist cannot claim the unique superiority of his own method as a scientist--rather he must do so as a philosopher!

For some thoughtful discussions that explore this further, check out the Vertias forum.

We Were Made for Both
Now that we've sketched some of the boundaries of scripture and science to prevent us from the ditches on either side, there is one final danger that we ought to avoid and that is the danger of thinking the study of scripture and science are altogether unrelated: that one can walk the road of scientific discovery and not have it affect her life or faith, or that one can study scripture and not have it affect the way she makes sense of the universe.

Now I understand the attraction to such a view: as highlighted above scripture has been inappropriately used to stifle scientific discovery and people have wrongly called on science to stifle faith. It is no wonder then that many have been drawn to the idea that science and religion are two different lines of inquiry that have authority to speak to different kinds of questions; they are non-over lapping magesteria.

Broadly, there are some features of this thinking are quite helpful. We shouldn't expect scripture to answer every scientific question that we may have nor should we expect to conduct a scientific experiment to verify, say, the doctrine of the trinity. Some truth can only be known through special divine revelation (the book of scripture) and some truth has been left to general revelation (the book of nature). In fact, scripture encourages us to seek out those truths that have been hidden in the creation (Proverbs 25:2).

But these are not to remain isolated, independent ventures. Reflecting on the natural world led David to sing of the Creator (Psalm 19), and yet, in the same Psalm, he moves naturally to a praise of the Torah. In another Psalm, David recorded how it was his study the Torah that led him to be wiser than the established authorities (119:99-100)--an experience that both Luther and Kepler can identify with.

The greatest problem with the idea of non-overlapping magestria is that it forgets that we ourselves stand at the intersection: dirt created in the image of God. We are physical beings, but also theological beings. To divide our study of the world from our study of God is against our very nature. And standing in this intersection, we are not alone. Throughout history God has acted concretely in the physical world. Parting waters, healing the sick, and bringing down strongholds. Above all, in the incarnation, God Himself in the person of Jesus is found inhabiting our physical world as a real man. Notably, after His resurrection, the tomb was empty--He was raised and enthroned in heaven with a Man's body. The Christian cannot just consider God as an abstraction or philosophical exercise detached from our world, and hence, our study of the world. The scars on His hands won't allow for that. The Creator is forever connected with His creation.

What the Bible Teaches about Islam, Allah, and Judgement

Recently, an evangelical college placed a professor on leave for expressing that Muslims and Christians worship the same God. Numerous other news reports have surfaced highlighting an increased concern in some Christian communities regarding Islam. While my own faith community seems to continue on rather positive terms with our Muslim friends, we are not immune from the influence of fear. For the benefit of my own community and that of friends looking on, I took a moment to share some thoughts on what Scripture has to say about some of the current questions I hear being asked about Islam, Allah, and Judgment.

Over the last couple weeks, as I've been reading through the Qur'an, one thing has become clear: Allah is a name for the God of Abraham. This makes sense--Islam traces its lineage to Ishmael, son of Abraham, just as Judaism traces its history to Isaac, son of Abraham. While Genesis gives Isaac a special position among the sons of Abraham--he is the promised child whose lineage Messiah would come from--Ishmael is also favored by God and it is promised that he too will become a great nation (Genesis 21:18). Interestingly, Ishmael had 12 sons, just as Isaac did (Genesis 25:12-17). While Ishmael and his sons move to the east, the Hebrew Scriptures tend to have a positive view of them, for instance, associating wisdom with those in the East (1 Kings 4:30). Moreover, a number of righteous characters such as Job (Job 1:3) and Moses' father-in-law Jethro, a priest of Midian (modern Saudi Arabia), are from the East and are presented as offering true worship to the true God. This background helps explain the presence of wise men from the East at the opening of Matthew's gospel (an excellent sermon on this).

Recently, some Christian's have argued that Allah is not the same as the Christian God because Islam's Shahada which affirms the oneness of God in declaring that there is no God but Allah is inconsistent with the Christian understanding of God as trinity. However, the Hebrew Shema which plays a central role in Judaism, and was cited by Jesus as the climax of Torah, makes a very similar declaration ("the LORD our God, the LORD is one"; see Deuteronomy 6:4-9). Significantly, Christians have never held to the position that Jews who reject the the doctrine of the trinity worship a different God. Rather, the Christian community has readily acknowledged that the Hebrew Scriptures say very little to suggest the God of Abraham, YHWH, has a triune nature (although, through the lens of the New Testament, one can see suggestions of it present). Therefore, rather than claim that those who worship YHWH worship a different God, Christians have always held that they worship the same God as the Jews, but that something new (and incredibly important) has now been revealed about this God since the incarnation of Christ and the outpouring of the Holy Spirit.

Indeed, the Qur'an outright rejects the divinity of Jesus. It presents God as One Person, rather than the Christian conception of God as three-Persons-yet-One. Here there is an authentic disagreement between Christians and Muslims, just as there is authentic disagreement between Christians and most Jews over the identity of the Person of Jesus. But all three groups worship the God of Abraham, the Creator of heaven and earth. Christians believe their Muslim and Jewish friends have missed a most important Revelation of this God, but that doesn't change the fact that all three groups worship the same God. Moreover, in Christian history there have been many great individuals such as Isaac Newton, or in the early Advent movement, James White and Uriah Smith, who, at least for a time, rejected the doctrine of trinity. Of course, looking back we might lament that they did and even say they took a heretical position, but we still regard them as worshipers of the true God.

In addition to trinity, there seems to be another factor at play in many of these conversations: eschatology, that is, the theology of last day events. You see, Revelation describes a series of battles between various political/religious groups resulting in the persecution of the righteous and leading up to the return of Christ. Many of these battle scenes are described with references to Israel and middle eastern geography and therefore, especially in recent decades, some Christians have seen various wars in the middle east as fulfilling these prophecies with Islam fulfilling the role of the antichrist figure in Revelation. There are, however, a number of problems to this view. Chiefly, this is a selective (and rather modern) reading of apocalyptic prophecy that disregards the theological development of the New Testament. For you see, the New Testament presents Christ as the New Israel (just as He is the New Adam). What this accomplishes is it spiritualizes the blessings of the covenant to those who are "in Christ" (eg. 2 Corinthians 1:20). In particular, this means the references to Israel and Mediterranean wars should not be read in the sense of literal wars in the middle east, but through the lens of a spiritual conflict not limited to a particular geography. You can read about this in The Deep Things of God and The Israel of God in Prophecy.

Of course, there is a spiritual system of confusion and persecution described by terms such as "Babylon", "the harlot", and "the beast" described in the Revelation. But the Revelation consistently describes this system using Roman and, more incredibly, Christian language. Rome would have made sense since the original audience of the Revelation was facing persecution from Rome for their refusal to participate in the cult worship of the Roman emperor. The fact that Christian language is also used to describe this system is more surprising (here are some study guides that walk through this), but it is consistent with the teachings of Paul and Jesus that the greatest danger the Church faced is that one day it would transform from a persecuted people to a persecuting people. In short, Revelation isn't warning against some other faith such as Islam when it describes a system of massive religious confusion and persecution. Rather, it is warning against what Christianity can become, especially when it lays hold of political force. Much of Christian history is a sad testimony to the accuracy of Revelation's prediction.

Fascinatingly, the Qur'an seems to have recognized this transformation of Christianity away from a pure faith:

"If only the People of the Book [Christians] had faith, it would be best for them. Among them are some who have faith, but most of them are perverted transgressors." [3:110] 

"Not all of them are alike: of the People of the Book are a portion that stand for the right. They rehearse the Signs of Allah all night long, and they prostrate themselves in adoration. They believe in Allah and the Last Day. They enjoin what is right, and forbid what is wrong, and they hasten in emulation in all good works. They are in the ranks of the righteous." [3:113-114]

Notice, the Qur'an maintains a high regard for those who maintained an authentic faith, anticipated the last day, and lived righteous lives. As I look back at history, I can identify with those who rejected the Romanization of the Church into an empire, desiring a more authentic life of faith and obedience. Does this mean I agree with all of the teachings of the Qur'an? Not at all. The identity of the Person of Christ is central and I believe here the Qur'an gets it wrong. But I also see how Islam maintained other great teachings of the New Testament that the Christian Church largely disregarded for much of history, such as those highlighted in the passages above. Moreover, Protestants have long taken a favorable view of Islam if only because it seems the Protestant Reformation would have been quickly stopped if Turkish armies hadn't at a critical moment stole the attention of emperor Charles V long enough for the reformation to spread (see Great Controversy, Chapter 11).

Jesus taught his followers, "I have other sheep which are not of this fold; I must bring them also, and they will hear My voice; and they will become one flock with one shepherd." Notice, Jesus affirms that there are others that just as truly belong to Himself; moreover, He leaves the responsibility to Himself to guide them to Himself. What is the Christian's role in all this? At the end of the day, rather than seek to demonize or draw into question the worship of our Muslim friends, Christians should examine the purity of their own worship. Not only then will our good works lead others to glorify God (Matthew 5:16), but it will guard as against false security. After all, as Jesus reminded His disciples, simply knowing to call Him Lord does not constitute true worship:

"Not everyone who says to me, 'Lord, Lord,' will enter the kingdom of heaven, but only the one who does the will of my Father who is in heaven. Many will say to me on that day, 'Lord, Lord, did we not prophesy in your name and in your name drive out demons and in your name perform many miracles?' Then I will tell them plainly, 'I never knew you. Away from me, you evildoers!'" (Matthew 7:21-23)

Jesus' teaching of the Day of Judgement highlights not only that many who thought they were living in service of Him were in fact not, but also that many were serving Him without ever realizing it (see Matthew 25:31-46). I'll close with a reflection on this judgement scene from The Desire of Ages:

How surprised and gladdened will be the lowly among the nations, and among the heathen, to hear from the lips of the Saviour, "Inasmuch as ye have done it unto one of the least of these My brethren, ye have done it unto Me"! How glad will be the heart of Infinite Love as His followers look up with surprise and joy at His words of approval! 

But not to any class is Christ's love restricted. He identifies Himself with every child of humanity. That we might become members of the heavenly family, He became a member of the earthly family. He is the Son of man, and thus a brother to every son and daughter of Adam. His followers are not to feel themselves detached from the perishing world around them. They are a part of the great web of humanity; and Heaven looks upon them as brothers to sinners as well as to saints. The fallen, the erring, and the sinful, Christ's love embraces; and every deed of kindness done to uplift a fallen soul, every act of mercy, is accepted as done to Him.

Ellen White: Top 10

There are a few authors who have had a disproportionate influence on my life. Often, I appreciate them for their perspective on a specific theme. An exception is Ellen White--a name especially well-known to many in my faith community. Her writings have profoundly influenced my views of life, God, education, health and a number of other topics. Here's a collection of the 10 chapters I revisit most often and quotes from them that I frequently think about.

1. God with Us: http://www.whiteestate.org/books/da/da1.html
   "Our little world is the lesson book of the universe."
   "Only by love is love awakened."
2. Help in Daily Living: http://www.whiteestate.org/books/mh/mh40.html
   "What a man is has more influence than what he says."
   "Worry is blind and cannot discern the future; but Jesus sees the end from the beginning. In every difficulty He has His way prepared to bring relief. "
3. Source and Aim of True Education: http://www.whiteestate.org/books/ed/ed1.html
   "Our ideas of education take too narrow and too low a range. There is need of a broader scope, a higher aim. True education means more than the pursual of a certain course of study. It means more than a preparation for the life that now is. It has to do with the whole being, and with the whole period of existence possible to man. It is the harmonious development of the physical, the mental, and the spiritual powers. It prepares the student for the joy of service in this world and for the higher joy of wider service in the world to come."
   "Love, the basis of creation and of redemption, is the basis of true education."
   "Unselfishness underlies all true development."
4. Least of These My Brethren: http://www.whiteestate.org/books/da/da70.html
   "Those whom Christ commends in the judgment may have known little of theology, but they have cherished His principles. Through the influence of the divine Spirit they have been a blessing to those about them."
   "We need not go to Nazareth, to Capernaum, or to Bethany, in order to walk in the steps of Jesus. We shall find His footprints beside the sickbed, in the hovels of poverty, in the crowded alleys of the great city, and in every place where there are human hearts in need of consolation."
   
5. It is Finished: http://www.whiteestate.org/books/da/da79.html
   "God could have destroyed Satan and his sympathizers as easily as one can cast a pebble to the earth; but He did not do this. Rebellion was not to be overcome by force. Compelling power is found only under Satan's government. The Lord's principles are not of this order. His authority rests upon goodness, mercy, and love; and the presentation of these principles is the means to be used. God's government is moral, and truth and love are to be the prevailing power."
6. Helping the Tempted: http://www.whiteestate.org/books/mh/mh10.html
   "God rejoices to bestow His grace upon us, not because we are worthy, but because we are so utterly unworthy. Our only claim to His mercy is our great need."
   "'We are saved by hope.' The fallen must be led to feel that it is not too late for them to be men."
   "With a sense of our own infirmities, we shall have compassion for the infirmities of others."
7. Why was Sin Permitted? http://www.whiteestate.org/books/pp/pp1.html
   "'God is love.' His nature, His law, is love. It ever has been; it ever will be."
   "Since only the service of love can be acceptable to God, the allegiance of His creatures must rest upon a conviction of His justice and benevolence."
8. God's Purpose for His Church: http://www.whiteestate.org/books/aa/aa1.html
   "Enfeebled and defective as it may appear, the church is the one object upon which God bestows in a special sense His supreme regard. It is the theater of His grace, in which He delights to reveal His power to transform hearts."
9. The Scriptures a Safeguard: http://www.whiteestate.org/books/gc/gc37.html
   "God will have a people upon the earth to maintain the Bible, and the Bible only, as the standard of all doctrines and the basis of all reforms. The opinions of learned men, the deductions of science, the creeds or decisions of ecclesiastical councils, as numerous and discordant as are the churches which they represent, the voice of the majority--not one nor all of these should be regarded as evidence for or against any point of religious faith."
10. God's People Delivered: http://www.whiteestate.org/books/gc/gc40.html
    "The mystery of the cross explains all other mysteries. In the light that streams from Calvary the attributes of God which had filled us with fear and awe appear beautiful and attractive."
11. If you're familiar with any of her writings, share your favorite chapter or quote in the comments below!

5 Lessons From the Ordination Debate

For the last few years, the Seventh-day Adventist Church has been engaged in a process of ongoing study and discussion to determine if we should allow for the ordination of women to the gospel ministry. To be clear, the Adventist Church has a long history of women serving as teachers and in other capacities--in fact, the Church was cofounded by a woman, Ellen White, and we still hold her inspired counsel in high regard. Also, since the first days of the movement we've had female pastors. Rather, the debate is centered around if the specific practice of ordination should extend to women, where the Church publicly recognizes someone's call to ministry and grants them authority to do things such as plant a local church, perform wedding ceremonies, and so on.

Next month, the Adventist Church will gather as a global Church in general conference (GC). We do this every five years, where thousands of representatives come together to decide issues of Church business, policy, and, occasionally, vote on statements of doctrine. This is where we'll decide what to do with the question of women's ordination. We'll vote either to (a) prohibit it or (b) allow various divisions of the Church to decide for themselves on this matter. There's a checkered history of this matter being brought up in previous GC sessions and various unions and divisions taking actions on it, but I won't recap that here. Suffice it to say, there's a lot of discussion and excitement around this topic.

As I've been listening and watching, I've recognized 5 areas where we need to experience radical growth as a community. My hope and prayer is that this controversy will teach us the lessons we need to learn to face the challenges ahead. I'm confident we will through the Spirit's teaching and Christ's leading.

We Like to Argue
Adventists have a long history at debate and we've become pretty good at it. In the early days of the movement, an Adventist pastor would ride into town and challenge the local, say, Baptist or Methodist pastor to debate on a topic such as Sabbath. Entertainment options were limited in the late 1800s, so this typically drew quite the crowd. And when we found that we could more often than not win these debates, we thought it must be a pretty good approach.

But Ellen White disagreed. She offered some sharp criticism of those who actively seek out debates, urging that they be avoided whenever possible. Significantly, she observed, "With those who have educated themselves as debaters, there is great danger that they will not handle the Word of God with fairness" (Testimonies, Vol 5, p. 708).

She also warned more generally against "argumentative discourses", believing they eclipsed the far more important purpose of presenting "Christ and His matchless love" (1888 p. 822)

Yet, many Adventists have continued to covet the debate and 10-points-to-prove-them-wrong sermons. One minister, who I genuinely respect for his commitment to evangelism, has even done a series of debates against himself!

At least he won.

Now that women's ordination has become a topic of interest, my Facebook newsfeed has become filled with a superabundance of (lengthy) sermon series, seminar videos, and articles seeking to prove a particular position.

Unnecessary debates. Argumentative discourses.

I get it; this is important. We should talk about it. I'm not saying let's end all conversation.

In fact, it would be very unhealthy if no differences of opinion were expressed in our community, for that would mean we have abandoned the project of reformation:

When no new questions are started by investigation of the Scriptures, when no difference of opinion arises which will set men to searching the Bible for themselves to make sure that they have the truth, there will be many now, as in ancient times, who will hold to tradition and worship they know not what. (Testimonies, Vol 5, p.707)

However, what seems to have largely happened is that individuals have committed to a position--perhaps after hearing a favorite speaker present on it--and then they've sought to amass arguments in favor of that view and dismiss those contrary to it. (There are, of course, a few notable exceptions.)

One cannot listen to ten hours of presentations or read half a dozen articles advancing a particular side and trust them to accurately present the opposing view. Comparable time must be given to the voices on the other side.

Ultimately, we need to learn to respond to differences of opinion by a greater distrust of self and a greater willingness to search the scriptures with an open heart.

Moreover, all of our discourses must become centered on Christ and His matchless love. This isn't incidental to our theology. Rather, Adventist theology is a system of truth where all the teachings center on the character and work of Christ. 

The Sacrifice of Christ as an atonement for sin is the great truth around which all other truths cluster. In order to be rightly understood and appreciated, every truth in the Word of God, from Genesis to Revelation, must be studied in the light that streams from the cross of Calvary. (Gospel Workers, 315)

There is one great central truth to be kept ever before the mind in the searching of the Scriptures—Christ and Him crucified. Every other truth is invested with influence and power corresponding to its relation to this theme. (Manuscript 31, 1890)

Never should a sermon be preached, or Bible instruction in any line be given, without pointing the hearers to “the Lamb of God, which taketh away the sin of the world.” John 1:29. Every true doctrine makes Christ the center, every precept receives force from His words. (Testimonies, vol. 6, p. 54)

These are the two overarching goals of the Advent project that our pioneers spoke about: (1) discover what Scripture teaches, recognizing much has been distorted or lost sight of in the many years of Christian history and (2) center all truth in Christ. Let's get back to work!

We Need to Study Scripture Deeper
Some excellent Biblical study has been done with regard to the question of women's ordination. Quite a bit, actually. The Theology of Ordination Study Committee (TOSC) is a great place to start looking. However, this depth of study has largely failed to trickle down to how many individuals and ministries are engaging with this topic. Many have offered simplistic arguments or what they claimed to be the nail-in-the-coffin "proof texts", insisting that a plain reading of the text settles the question. However, our movement has always recognized that many passages don't lend themselves to a "plain" reading:

"Some portions of Scripture are indeed too plain to be misunderstood, but there are others whose meaning does not lie on the surface to be seen at a glance. Scripture must be compared with scripture. There must be careful research and prayerful reflection. And such study will be richly repaid." (Steps to Christ, p.90)

Currently both sides are criticizing the hermeneutics that the other side is using (from the con-side here and from the pro-side here), while both continue to use arguments that are simply not faithful to the text. Here are a few noteworthy examples:

• [PRO] Women have an equal right to ordination: Except, ordination isn't a right. Moreover, ministry isn't a right. When you read about Paul's calling to ministry, it is clear that he didn't have a right to become an apostle, but an obligation and privilege. The Spirit calls whom He wills. He has a right to call whomever He desires. Here's an excellent sermon that engages with this a bit further.
• [PRO] Women should be paid the same as men: I agree and it is deeply unfortunate that the current arrangement of ordaining male pastors while only commissioning female pastors has often led to unequal compensation. Paul clearly taught that ministers have a right to be fairly compensated (1 Cor 9). This needs to be addressed. Immediately. But it doesn't, in itself, necessitate the ordination of women. There are other ways to guarantee equal pay.
• [CON] Paul said, "I do not prevent a women to teach or exercise authority over a man": This is, simply put, a tough passage. However, even if we try to take it at face value, devoid of any context, it would say too much. In particular, it would say that women can't teach. This is inconsistent with the New Testament witness of female teachers (such as Prisca) and the long history of female teachers in the Adventist Church, which nobody is currently contesting. Some try use this to argue that Paul is just preventing women from authoritative teaching positions (and still permits non-authoritative teaching--whatever that means); however, this seems to directly contradict our understanding of the authoritative nature of Ellen White's writings. In fact, this verse was used as a criticism that Ellen White had to overcome during her ministry. This should indicate that we need to carefully study the context and situation of Paul's writing. From my personal study, here's what I've found.
• [CON] A women can't be the husband of one wife: Paul wrote that an overseer or deacon ought to be "the husband of one wife". Therefore, the argument goes, since a woman can't be the husband of one wife, she shouldn't be ordained. Yet, Paul himself was unmarried and ordained (Acts 13:1-2). Moreover, to read an implicit assumption here that the individual must be male would be inconsistent with how we read the rest of Scripture. For instance, when we read the last commandment prohibits a husband from coveting another man's wife, we understand that this applies to women not coveting other woman's husbands, as well.Instead of using this text to answer the question of women's ordination--which Paul was in no way addressing--we should ask what Paul was addressing (such as the sexual immorality prevalent in the church) and understand from there why he gave this qualification.
• [CON] God only ever chose men to be priests in the Old Testament: Problem: Pastors aren't priests. There may be good reason for, say, the Catholic Church not to ordain female priests, but Protestants don't have a priestly class. Rather, we affirm that Christ is the great High Priest that the Old Testament priesthood was anticipating and we hold to the New Testament model of a priesthood of all believers in Him.
• [CON] It's contrary to the creation order: Here, one appeals to Paul's statements that a husband is head over his wife and notes that Paul couples this with creation language. In particular, he says things like, "For man was not made from woman, but woman from man. Neither was man created for woman, but woman for man." Some have taken this to mean that a man has authority over his wife. However, this is especially problematic for Adventists because when Jesus says things like, "Sabbath was made for man, not man for the Sabbath", we certainly don't take that to mean that man has authority over the Sabbath! Rather, "the Son of Man is Lord of the Sabbath." Some really careful study should be done to determine what exactly Paul means by his headship language. Especially since right after arguing that woman (Eve) came from man (Adam), Paul reminds his readers in 1 Corinthians 11 that every man came from a woman--notably his mother!
  Yet, whatever conclusion one comes to, the fact remains that Paul limits this language of headship to the relationship between a husband and wife. Some try to argue that a pastor/overseer is head of the Church, and women can't be heads, but this logic isn't present in any of Paul's arguments. Rather, Paul consistently reserves the title head of the Church for Christ alone.

Sure, one can weave together some of the above arguments and verses to make a case either for or against, but when we do so, we are using Biblical language in a way that is alien to how the authors of Scripture used it. We shouldn't open up a letter of Paul and demand it answer the questions we may have about women's ordination, because then we've already brought the assumption that it is saying something about women's ordination.

We need to learn to let Scripture answer the questions that it is addressing, not the questions we want it to address.

We're Misusing Ellen White 
I've seen numerous individuals appeal to statements of Ellen White to settle this debate. There are two problems with this.

First, I deeply appreciate the counsel of Ellen White. I believe it is an incredible, valuable gift to the Church, "But God will have a people upon the earth to maintain the Bible, and the Bible only, as the standard of all doctrines and the basis of all reforms" (Great Controversy, p. 595). Those are her words. So if we want to be those people of God she describes, we can't expect her to do the work of Biblical study on this one for us. Significantly, there were a number of controversies in her day that she refused to settle, insisting we let Scripture alone settle them.

The second reason this is problematic is because Ellen White intentionally avoided speaking on the issue of women's ordination. In 1881, a motion was presented to the general conference to permit the ordination of women. It was moved to committee and never followed up on. However, some continued to inquire what Ellen White's position on it was. Here's her personal secretary's response:

"Sister White, personally, was very careful about expressing herself in any wise as to the advisability of ordaining women as gospel ministers. She has often spoken of the perils that such general practice would expose the church to by a gainsaying world; but as yet I have never seen from her pen any statement that would seem to encourage the formal and official ordination of women to the gospel ministry, to public labor such as is ordinarily expected of an ordained minister."
“This is not suggesting, much less saying, that no women are fitted for such public labor, and that none should ever be ordained; it is simply saying that so far as my knowledge extends, Sister White never encouraged church officials to depart from the general customs of the church in those matters.”
[C.C. Crisler; June 16, 1916]

Notice, she very carefully avoided addressing it. Good luck looking for that this-settles-it quote! Moreover, the fact that she felt comfortable remaining silent means we probably shouldn't think of this as a moral issue or pillar of the faith.

We need to respect Ellen White's counsel and we need to respect her silence.

We Don't Know What to Do About Culture
Culture seems to always come up in these discussions. Many have tried to frame the entire debate in terms of faithfulness to Scripture verses conformity to culture.

However, we just noted in the section above that women's ordination was a live issue in the 1880s. One cannot therefore claim it is simply the Church being carried away with the feminist movement. Moreover, we shouldn't assume that the right position is always the position that seems most contrary to the trends in culture. Yes, there is always a danger of being swept along with the current of the times. But there is also the danger that we become reactionary against culture. Either way, culture is dictating our moves. An example may help illustrate this.

Over the last century or two, higher criticism has been catching on as a way of reading and understanding Scripture. In essence, this approach removes any supernatural aspect from the creation of Scripture, seeing it entirely as a product of the societies that the authors inhabited. As such, when a prophecy is encountered that is later fulfilled, it is assumed that it must have been written after the event that it's describing.

Many Evangelicals, troubled by this attack on the authority of Scripture, responded by developing a view that God dictated every word of  Scripture. This counter-cultural position directly addressed their concerns of higher criticism.

So which side did Adventism fall on? Did we go with culture? Or did we go with the counter-cultural position?

Neither.

Adventists believe in thought-inspiration, that God inspired the thoughts of the authors of Scripture which they were free to express in words of their own choosing. This recognizes a cooperation between the human and divine. We reject higher criticism because it leaves no room for the divine agent, yet we also reject word-inspiration because it leaves no room for the human agent:

"The writers of the Bible were God's penmen, not His pen... It is not the words of the Bible that are inspired, but the men that were inspired. Inspiration acts not on the man's words or his expressions but on the man himself, who, under the influence of the Holy Ghost, is imbued with thoughts. But the words receive the impress of the individual mind." (Selected Messages, Bk 1, p. 21)

Notice how this description carefully avoided both extremes. Similarly, today we shouldn't simply accept a view because it appears to stand up against trends in culture that may concern us. In seeking to avoid falling into the ditch on the left, we may end up in the ditch on the right.

There's another problem in the way we discuss culture: we fail to recognize that culture is often a valid consideration for how we do things. Recall that Ellen White, as the statement from her secretary above reveals, stayed quiet on the issue of women's ordination because she was afraid of what the "general practice would expose the church to by a gainsaying world".

She knew ordaining women wouldn't be popular in late nineteenth century America and she didn't want the practice to hamper the mission of the Church.

Therefore, it is altogether reasonable for one to suspect that there may be good reason to consider ordaining women if the culture has changed so that it would no longer hurt the mission of the Church. Even more-so if one believes it would help the Church's mission in that part of the world.

Now, that's not to say we end the discussion there. Deep Biblical study should be done to see if the practice is in harmony with Scripture. It's simply to recognize that our decisions shouldn't be dictated by a knee-jerk reaction against the culture we live in.

We Need to Show More Love
This last observation is probably the most important of them all.

In the midst of our debates over what head means in 1 Corinthians 11, we must demonstrate that we're committed to the unity of 1 Corinthians 12 and have made our top priority the love of 1 Corinthians 13.

This means we abandon our suspicion of one another. This means we continue to respect and serve alongside those who are of another opinion. This means we actually like people we disagree with. More than that, we trust them. We think higher of them than we do of ourselves.

Rather than advance a narrative that the foundation of the Church is threatened, we abide in the promise that Christ has built the Church on an unshakable foundation and He will protect it from the very gates of hell (Matthew 16:18). There's no reason to let fear divide us.

I'll close with this word of counsel:

Strive earnestly for unity. Pray for it, work for it. It will bring spiritual health, elevation of thought, nobility of character, heavenly-mindedness, enabling you to overcome selfishness and evil surmisings, and to be more than conquerors through Him that loved you and gave Himself for you. Crucify self; esteem others better than yourselves. Thus you will be brought into oneness with Christ. Before the heavenly universe, and before the church and the world, you will bear unmistakable evidence that you are God’s sons and daughters. God will be glorified in the example that you set. 

The world needs to see worked out before it the miracle that binds the hearts of God’s people together in Christian love. It needs to see the Lord’s people sitting together in heavenly places in Christ. Will you not give in your lives an evidence of what the truth of God can do for those who love and serve Him? God knows what you can be. He knows what divine grace can do for you if you will be partakers of the divine nature. (Testimonies, Vol. 9, p. 188)

The world is dying to see a demonstration of this love. What an awesome opportunity we have to show it.

Paul, Women, and the Command to Remain Quiet

"I do not permit a woman to teach or to exercise authority over a man; rather, she is to remain quiet." (1 Timothy 2:12)

I've long wondered why Paul wrote this to Timothy. Perhaps you have too.

If so, you should know we're not the first ones to recognize that some teachings of Paul are tough to understand--and easily mishandled.

Far from it.

Discussing Paul's letters, his friend Peter wrote, "There are some things in them that are hard to understand, which the ignorant and unstable twist to their own destruction, as they do the other Scriptures." (2 Peter 3:16)

Wow! Serious stuff. So what are we to do?

In one of my all time favorite books, Ellen White notes: "Some portions of Scripture are indeed too plain to be misunderstood, but there are others whose meaning does not lie on the surface to be seen at a glance. Scripture must be compared with scripture. There must be careful research and prayerful reflection. And such study will be richly repaid." (Steps to Christ, p.90)

This seems to be one of those cases.

Recently, I decided to dig a little deeper. Today I concluded that Paul is in no way the misogynist some of his critics have made him out to be. Actually, if anything, Paul was a counter-cultural advocate of women. Here's how I arrived at this conclusion*:

If you haven't yet, you may like to open up to 1 Timothy and follow along.

Paul's first letter to Timothy opens with him explaining that there are some teaching the law who don't know what they're talking about (1:7). Their problem is that they deviated from what the whole thing is about: "The aim of our charge is love that issues from a pure heart and a good conscience and a sincere faith" (1:5).

We later learn that these unqualified teachers includes a group of women who are also described as needing to learn and shouldn't have the authority to teach (2:11-12). Notice, Paul also encourages them to "continue in faith and love and holiness, with self-control" (2:15).

The structure of the letter helps us recognize that Paul is discussing a particular group of women that are part of a larger problem in Ephesus that Timothy needs counsel on how to handle. Paul is writing to address "certain persons" (1:6), not all people. We cannot divorce his counsel from the situation that called for it.

Who are these women? They are likely new to the community (thus 3:6) and thought they could immediately start teaching because they had a high status in society (2:9). But Paul doesn't care about their status; he esteems people based on their character and actions (2:10). Thus he tells them to hold off on teaching (in the Greek, "I do not *now* permit...") to continue learning respectfully (2:11).

It is noteworthy that there is one other time when Paul commands a group of individuals to exercise ἡσυχία (translated in 1 Tim 2:11-12 as quietness or silence) and that's to a group of Thessalonians that Paul describes as "disorderly, not working as all, busybodies" (2 Thess 3:11-12). Similarly, Paul commanded them to work in quietness.

In neither case is Paul's concerned about gender. Rather, he's addressing situations of disorderly conduct--one case largely involves men, the other women.

Next in his letter to Timothy, Paul appeals to the story of Eve being deceived by the serpent to serve as a potential warning of the seriousness of the situation. Why cite Eve? Because the situation occurring in Ephesus involves people incorrectly teaching the law and Eve is the ultimate example of someone misquoting the law. In her conversation with the serpent, Eve stated that the commandment said, "You shall not eat of the fruit of the tree that is in the midst of the garden, neither shall you touch it, lest you die" (Genesis 3:3). However, that's wrong. She added the clause "neither shall you touch it" (compare with Genesis 2:16).

Ellen White perceptively explains how this led to her deception:

In Eve’s controversy with the serpent, she added “Neither shall ye touch it.” Here the subtlety of the serpent appeared. This statement of Eve gave him advantage; he plucked the fruit and placed it in her hand, using her own words, He hath said, If ye touch it, ye shall die. You see no harm comes to you from touching the fruit, neither will you receive any harm by eating it. (Confrontation, p. 14)

By appealing to this story, Paul isn't teaching that Eve was deceived because she was a woman. He is making the point that she was deceived because she didn't properly handle the law--the very situation that Timothy was dealing with (1 Tim 1:7). 

By also mentioning Adam, who was formed before Eve and wasn't deceived (1 Tim 2:13-14), Paul seems to be softly rebuking those in the community who may have been around longer than this group of women and had a better understanding of the law, but who, like Adam, went along with the situation instead of lovingly addressing it.

Yet, to be clear that he isn't just Eve-bashing, Paul reminds his readers that salvation came through her offspring, the Messiah (1 Tim 2:15; compare Gen 3:15). Paul also seems to have high hopes for what can come out of this controversy.

What Paul does in the next part of his letter is incredible.

Significantly, the very things Paul instructs the women to learn are included in the qualifications for servant leadership positions (1 Tim 3). For instance, Paul only mentions κόσμιος (good conduct) twice in all of his writings: once when describing what this group of women should learn (2:9) and again when describing what attribute the overseer of a church should have (3:2). Paul also, right before calling out this group of women, had called out a group of men and told them that they needed to learn some things too (2:8), which he also includes in his list of qualifications (1 Tim 3)--such as how to control their anger. Also, Paul lists "husband of one wife" to condemn bigamy and affirm the value of marriage (contrast with 1:10, 4:3). The point is he is unpacking what it means to be "above reproach" (3:2) in light of recent situations in the church.
By blending the instruction that he had just given to both the group of men and the group of women to form the list of qualifications, Paul accomplishes two things. First, he prevents those causing the problem--both the group of men and the group of women--from taking over leadership positions in the community. Second, however, he suggests that in time, those very ones causing the problems may become qualified men and women to take over those roles. Paul's solution is both practical and redemptive.

Does Paul really envision both men and women serving as leaders? Indeed, elsewhere he mentions women who were serving in leadership roles, such as Phoebe serving as a deacon and Junia serving as an apostle (Rom 16:1-6). Granted, some scholars argue that there is some ambiguity of the Greek here that might allow for alternative readings of the roles of these two particular women. Whatever the case, there's no ambiguity when it comes to Prisca. Acts records Paul met Aquila then his wife Prisca (Acts 18:2-3). But then Acts goes on to address them as Prisca and Aquila--breaking the cultural trend by putting the wife's name first (Acts 18:18, 26). Of note, the context is them teaching Apollos, indicating that Prisca was leading out in the teaching.

Similarly, in his earliest letter, Paul sends greetings from Aquila and Prisca (1 Corinthians 16:19), but moves on in later letters to addressing them as Prisca and Aquila (Romans 16:3, 2 Timothy 4:9), affirming her role as a teacher and challenging his culture.

Granted, as revolutionary as Paul was, he was just following the example of Jesus who intentionally challenged the status quo by elevating women and giving them roles of supreme importance. For instance, after His resurrection, Jesus first appears to a group of women and tells them to spread the word that He had risen, despite the fact that the testimony of women was considered unreliable.

Moreover, Paul was responding to the sacrifice of Christ, since he believed the Cross-event gave all people equal standing before God. In another letter, Paul taught, "There is neither Jew nor Greek, there is neither slave nor free, there is no male and female, for you are all one in Christ Jesus." (Galatians 3:28)








*Note well, my understanding of Scripture is constantly growing, especially on some of these less plain passages. "We see in a mirror dimly." If you walk away with a different understanding, that doesn't bother me in the least. I agree with White: "We cannot then take a position that the unity of the church consists in viewing every text of Scripture in the very same light." Here's an excellent article that explores further how Ellen White and the early Adventist Church promoted unity while allowing for some theological diversity.

Word Count

Do you have a favorite Christian author? Growing up I enjoyed the novels of C.S. Lewis and in high school a friend introduced me to his masterpiece Mere Christianity. But it wasn’t until college that I discovered the books of my favorite author, the 19th century Christian leader Ellen White. Consistently, I’ve found her writings (such as Steps to Christ and The Desire of Ages) to be gifted with exceptional clarity and insight.

Wanting to better understand what makes them so powerful, I recently did an analysis of all of White’s books, articles, manuscripts, and other released writings. What I found amazed me. It is presented in the graphic below where the font size of each word corresponding to how often she employed it throughout her lifetime (that is, a word has twice the font size if she used it twice as often).

Far above anything else, she exalted Christ. Yes, she wrote about many important Biblical themes such as obedience and health, but she always kept these things in the shadow of Christ. In her own words,

“There is one great central truth to be kept ever before the mind in the searching of the Scriptures—Christ and Him crucified. Every other truth is invested with influence and power corresponding to its relation to this theme.” (Manuscript 31, 1890)

Raw data (word count): Christ (83,441), Jesus (41,563), Love (33,924), Faith (30,587), Character (22,799), Law (15,393), Grace (14,948), Prayer (12,372), Health (11,533), Service (11,196), Salvation (11,143), Bible (10,304), Hope (9,822), Gospel (9,528), Judgment (8,298), Sabbath (7,265), Obedience (6,626), Commandments (6,303), Dress (2,476), Diet (2,375).

Revealing Us

This is the third in a three part series on the significance of the cross. Be sure to check out part one, Revealing God, and part two, Revealing the Enemy.

In the last two posts we’ve noticed two progressive revelations in John’s account of the gospel: the revealing of the love of God and the unmasking of the selfish deception of the Enemy. Both came to a climax at the cross.

Does John’s gospel account have anything to reveal about us?

I believe it does.

Perhaps already we find ourselves identifying with the tension of the great controversy we’ve discovered between the God of self-giving love and the Enemy of selfish destruction.

I call it a tension since we regularly make choices on both sides. Although we might find ourselves drawn to the concept of perfect alignment with God’s love, experience suggests we’re stuck with selfishness, pride, and all other sorts of anti-love characteristics which places us in opposition to God.

Are we fated to live a double-life? Is complete allegiance to God impossible?

Honestly, these are questions I deeply wrestle with, perhaps even more than the question of why is there suffering. But I believe there’s a noteworthy progression in John’s gospel account that begins to suggest an answer.

It’s a progression of how Jesus related with his disciples. Notice how he addressed them:

First, he calls them “servants” (Jn. 13:16).

Then, he calls them “disciples” (Jn. 13:35).

Later, he calls them “friends” (Jn. 15:15).

Finally, he calls them “brothers” (Jn. 20:17).

A servant’s loyalty extends only as far as it benefits himself, a friend’s loyalty is a bit better, but a brother’s loyalty has no limit. Moreover, while a servant may look nothing like his master, brothers resemble one another.

This tells me something: If I stick with Jesus, I’ll grow to resemble him more. In time, all my choices will come to reflect the love of God. I find this incredibly encouraging.

How is this possible?

Again, we look to the cross. Notice it was not until after the death and resurrection of Jesus that he called his disciples “brothers”:

“Jesus said… Go to my brothers and say to them, ‘I am ascending to My Father and your Father, and to My God and your God” (Jn. 20:16-17).

Something of incredible significance happened at the cross.

God’s love was revealed. The enemy’s selfishness was revealed. But also we were revealed.

Looking at the cross, we see what our selfish choices cost. We see what we deserve.

But also, we see what God in love gave. We see all our sin, guilt, and brokenness dealt with.

Then, free from the burden of guilt, now having a clear picture of God’s love, we’re able to live as Jesus’ brothers and sisters. As children of the God of love, we learn to live out His love.

Revealing the Enemy

This is the second in a three part series on the significance of the cross. Be sure to check out part one: Revealing God.

Last post, we saw in John’s gospel account the progressive unveiling of the love of God: Jesus’ miracles and teachings reveal the Father’s love with increasing clarity leading up the fullest revelation in the cross event.

But a question remains. If the picture of God we saw in Jesus is accurate–that He is a Person of absolute love–then why is the world so broken and suffering so pervasive?

This question has led some to conclude that there is another side to God; perhaps God isn’t always driven by love. But this isn’t Jesus’ answer. In the theology of Jesus all of God’s actions flow from the abundance of His love.

Rather, Jesus attributes the pain and mess of the world to another player altogether, the Enemy. And just as Jesus’ earthly life revealed God’s love, it also unmasked the Enemy’s selfishness. Note a few teachings about this Enemy:

Jesus calls him “the devil” (Jn. 8:44), which literally translates as “the accuser” or “the slanderer.” This helps explain why there is so much confusion about God.

Jesus describes the Enemy as a personal being, not just an evil force. Yet this being is fully given over to advancing destruction and deception: “He was a murderer from the beginning and does not stand in the truth, because there is no truth in him. When he speaks a lie, he speaks from his own resources, for he is a liar and the father of it.” (Jn. 8:44)

Jesus teaches that people, even respected religious leaders (Jn. 8) or professed followers of Jesus (Jn. 13:2), can align themselves with the Enemy’s plans.

Jesus calls him “the ruler of this world” (Jn. 12:31), explaining why our world is so broken.

We’re beginning to see how this being operates: He leads the cause for destruction and suffering, drafting others to join him, but through deception makes it appear God is really the guilty party.

Thus Jesus came to call out his lies.

But Jesus didn’t just use words. He performed miracles–healing the sick and raising the dead, showing that death and disease aren’t from the heart of God. Yet all this was just buildup to the greatest unmasking that happened at the cross.

Here’s how Jesus explained what took place on the cross: “Now is the judgment of this world; now the ruler of this world will be cast out” (Jn. 12:31).

In revealing the total self-giving love of God, Jesus also uncovered the devil’s selfishness. Jesus had called him a murderer, above any doubt, the cross verified this. Yes, there were human agents involved–corrupt religious and political leaders–but they were merely acting out the devil’s schemes.

Above we saw the devil works by destruction and deception. The cross signaled the end of his reign of deception. Now when one understands the cross event, she discovers the beauty of God’s love and the ugliness of the Enemy’s rebellion. Deception loses its power over her. And soon, when the message of the cross has been fully proclaimed, the Enemy’s reign of destruction will also be brought to an end.