Flat Earth? Doing the Math

Throughout the day, rapper B.o.B. has been tweeting "evidence" that the earth is flat, making him the most recent face of a growing flat earth movement. The ancient Greeks deduced that the earth is round by recognizing that the earth always casts a circular shadow on the moon and were even able to make a reasonably good approximation of the radius of the earth. Nearly 2,400 years later, it seems we should have universal consensus on the shape of the earth, especially since a live stream of the earth from space is just a click away.

What can account for the resurgence of flat earth truthers? B.o.B.'s question to Neil deGrasse Tyson, who had responded to some of the flat earth "evidence", is telling: "r u a mason?". Those who advocate for a flat earth are not just making a scientific claim, they're making the claim that the government, NASA, and the scientific community are controlled by an elite group attempting to systematically deceive the public on the nature of the cosmos. Moon landing: faked. Scientific authorities: compromised. Everybody else: sheep. Except, of course, that guy on YouTube who posted a video that exposes the whole thing. Pay some money and you can get his book on it, too.

This suspicion of scientific findings makes it very difficult to falsify the belief. Every piece of evidence one presents can simply be dismissed as part of the conspiracy. It makes for an interesting challenge: can one demonstrate that the earth is round without appealing to any modern authorities. (The ancient argument of the Earth's shadow on the moon is countered by a belief in an "anti-moon" that instead casts the shadow. It seems the ultimate conspiracy would be if a group of flat earthers faked a landing on this supposed anti-moon to prove its existence.)

Having posted a number of pictures that B.o.B. claimed demonstrated the non-curvature of the earth, a few hours ago he posted the challenge:

As a math guy, this caught my eye. It turns out the math required is just some basic high school geometry, making the flat earth movement the latest indicator that we need to do a much better job at improving our nation's math literacy. Here's one step in that direction.

New York Skyline

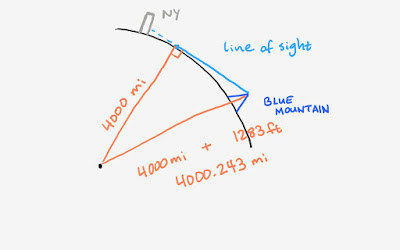
First of all, although the driving distance from Bear Mountain to Manhatten is 50 or 55 miles, it's only 40 miles away (map). Also, we'll be generous and approximate the earth to have radius 4000 miles (it is actually a bit less, but this will only bias the numbers in the flat earther's favor). So, how does the curvature of the earth affect one's view of the skyline? This diagram may help:

Notice when standing on top of blue mountain your line of sight only runs for so far until the curvature of the earth begins to obstruct your view. Using the Pythagorean Theorem we can calculate that distance to be 44.091 miles. Since New York is within 44 miles of Blue Mountain, on a clear day we can expect to see the entire skyline, just as the photo demonstrates.

But what if New York was 60 miles away? (Again, it's not. We're just running a hypothetical now.) We'd still be able to see the buildings, but the bottom portion would be hidden by the curvature of the earth. We can go ahead and calculate just how much would be hidden:

Another application of the Pythagorean Theorem gives us that just shy of 150 ft of the buildings would be covered (not too far off from B.o.B.'s claim of 170 ft). Notice, since many of the buildings in New York are many times that height, we would still expect to see the skyline.

Philadelphia Skyline

We can test other skyline claims similarly:

If you use the numbers given, then indeed we find that the lower 335 feet of the buildings should be hidden; however, since many buildings in Philadelphia are far taller than this, we should still expect to see the skyline. However, again the distance to the city has been overstated. The driving distance is less than 35 miles and the actual distance is closer to 30 miles (map). Being generous and using 35 miles takes the amount blocked to 200 feet. Interestingly, there happens to be a 60 foot fire tower on top of the hill. Standing on top of it, and using the actual distance to the city, it turns out less than the bottom 100 ft of the skyline is blocked by the earth's curvature. I encourage the interested reader to run the numbers for herself on other skyline photos that claim to prove the earth isn't curved.

Where's the Curve?

This'll be the last claim I engage with, bringing us full circle (like... a trip around the earth). Another application of Pythagorean's theorem shows us over a distance of 16 miles, the earth curves just shy of 170 ft. For perspective, the skyscrapes in those cities that you can barely see are many times that height. To think about it another way, the difference between the direction the skyscrapers are pointing in one city with the direction they're pointing in the other is 0.21°--a fraction of a degree. You see, the earth is big: just shy of 25,000 miles in circumference. So while the earth is curved, indeed, it is tough to notice on the scales that we're used to, although it is easily noticeable on a high altitude flight such as a concorde.

Many of the other arguments that B.o.B. posted are explained on the basis of misinformation (you can't see Polaris as you move into the southern hemisphere) or are based on a misunderstanding of science (how gravity works, what we mean when we call the earth an oblate spheroid, and so on). A good place to learn up on some of the relevant science is here and here.